Practice questions
page1 page2 page3 page4 page5 page6 page7 page8Logarithmic and Exponential Functions
34. Solve the following equations.
(a) $16^{2x+1}=64^{x+3}$
(b) $\log_4(2x+4)=3$
(c) $2^{x+3}=5^x$
(d) $\log_2(x)+\log_2(x-7)=3$
Solution:
(a).
First, rewrite the equation so that both the exponents have same base:
$(4^2)^{2x+1}=(4^3)^{x+3}$
$(4)^{2(2x+1)}=(4)^{3(x+3)}$
Now, the bases are the same, so the exponents should be the same:
$2(2x+1)=3(x+3)$
Now, solve for $x$:
$4x+2=3x+9$
Solving for $x$:
$x=7$
(b).
Write the logarithmic equation in exponential form:
$4^3=2x+4$
$64=2x+4$
Solving for $x$:
$x=30$
(c).
You cannot write this equation with same base on both sides. So take log on both sides:
$\log(2^{x+3})=\log(5^x)$
$(x+3)\log(2)=x\log(5)$
$x\log(2)+3\log(2)=x\log(5)$
Bring the $x$ terms together:
$x\log(2)-x\log(5)=-3\log(2)$
Factor out the $x$:
$x(\log(2)-\log(5))=-3\log(2)$
Divide $(\log(2)-\log(5))$ to get $x$:
$x=\dfrac{-3\log(2)}{\log(2)-\log(5)}$
After using the calculator:
$x=2.269$
(d).
First combine the two logarithms on the left:
$\log_2(x(x-7))=3$
Now, write in exponential form:
$2^3=x(x-7)$
$8=x^2-7x$
This is a quadratic equation, write in standard form to solve:
$0=x^2-7x-8$
i.e., $x^2-7x-8=0$
Factoring:
$(x-8)(x+1)=0$
Applying zero-product rule:
$x-8=0$ or $x+1=0$
$x=8$ or $x=-1$
$x=-1$ makes a negative number inside the logarithm, so this cannot be a solution.
So, the solution is
$x=8$
35. Rewrite the following expression as a single logarithm.
(e) $3\log_p(x)+\dfrac{1}{2}\log_p(y)-\dfrac{3}{2}\log_p(z)$
Solution:
Write the coefficients of log as exponents using the formula $\log_a{x^p}=p\log x$
$=\log_p(x^3)+\log_p(y^{1/2})-\log_p(z^{3/2})$
Combine them:
$=\log_p\left(\dfrac{x^3y^{1/2}}{z^{3/2}}\right)$
You can also write this as
$=\log_p\left(\dfrac{x^3\sqrt{y}}{\sqrt{z^3}}\right)$
36. Use the change of base formula to estimate the following logarithms to four decimal places.
(a) $\log_\pi(e)$
(b) $3\log_6 2.75$
Solution:
(a).
Use the change of base formula. Change the base to $e$ as there is an $e$ in the log. (You can also change the base to 10).
$\log_\pi(e)=\dfrac{\ln(e)}{\ln (\pi)}$
Since, $\ln (e)=1$:
$=\dfrac{1}{\ln (\pi)}$
$=\dfrac{1}{1.14473}$
$=0.8736$, after rounding to the four decimal places.
(b).
Use the change of base formula:
$3\log_6 2.75= 3\cdot \dfrac{\log(2.75)}{\log(6)}$
Use the calculator:
$= 3\cdot \dfrac{0.4393327}{0.778151}$
$= 3\cdot 0.564585$
$= 1.6938$
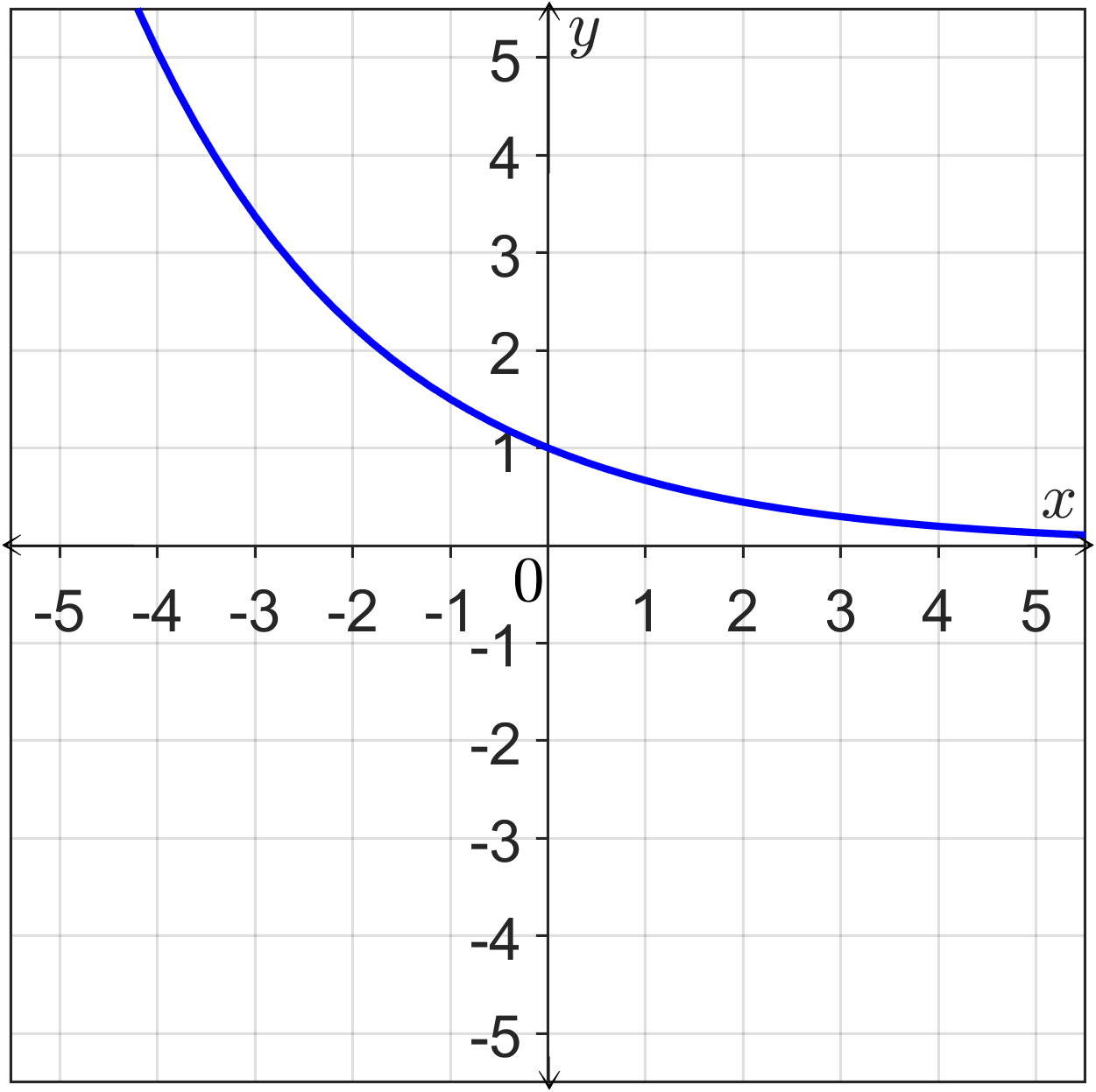
37. Graph.
(a) $y=\left(\dfrac{2}{3}\right )^x$
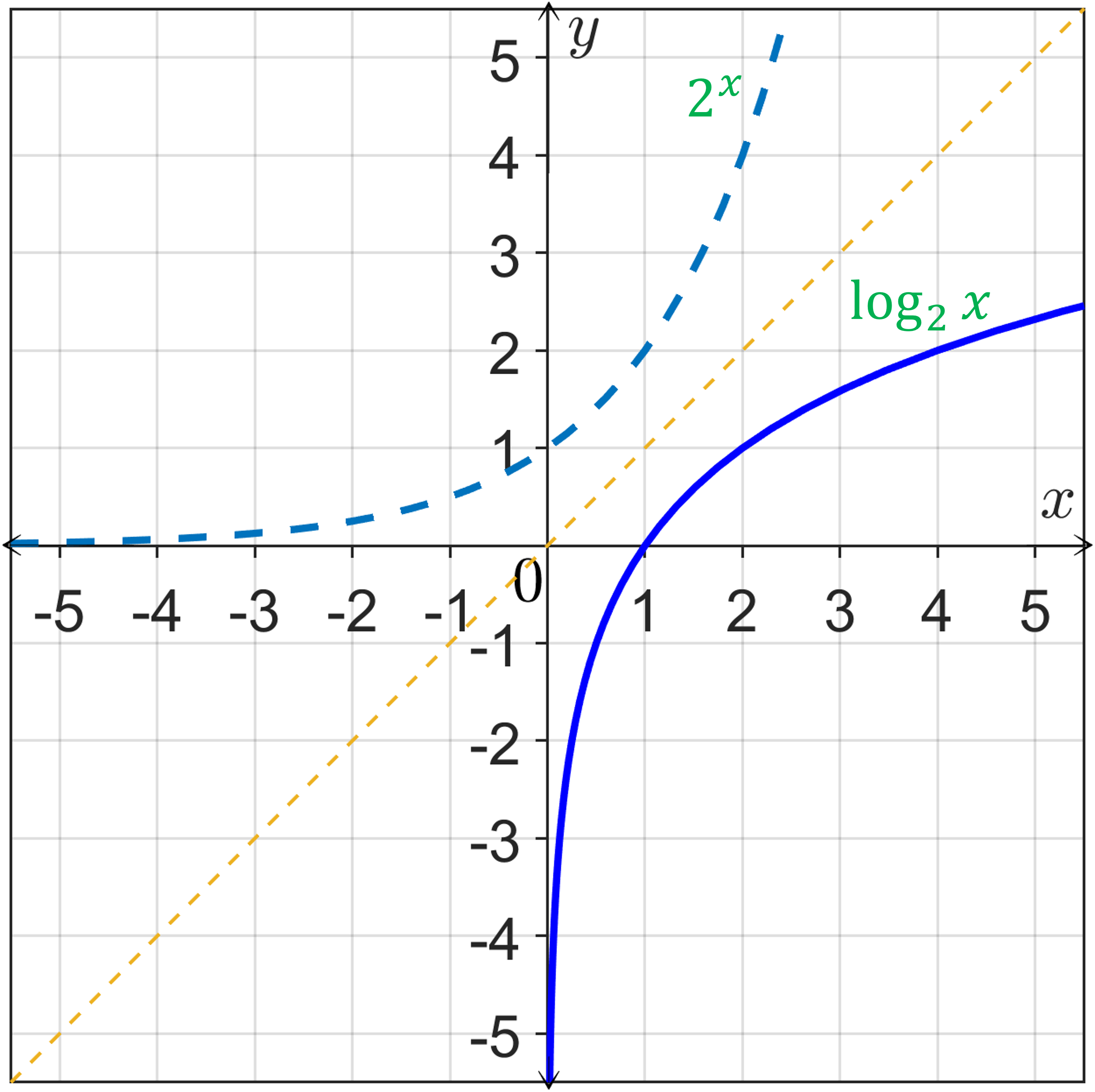
(b) $y=\log_2 x$
Solution:
(a):
Graph of $y=\left(\dfrac{2}{3}\right )^x$:
| $x$ | $y$ | $(x, y)$ |
|---|---|---|
| $-2$ | ||
| $-1$ | ||
| $0$ | ||
| $1$ | ||
| $2$ |
(b).
Logarithmic function is the inverse of the exponential function.
So, to draw the graph of $y=\log_2{x}$, draw the graph of $y=2^x$. Then draw a diagonal line as a mirror. The logarithmic function is the mirror image.
38. Solve the following problems using the interest formulas.
(a) What will be the amount A in an account with an initial principal of $4000 if interest is compounded continuously at a rate of 3.5% for 6 years? Also, how long does it take for the account to double?
(b) A college loan of \$29,000 is made at 3% interest compounded annually. After t years, the amount due, A, is given by the function $A(t)=29,000(1.03)^t$. If no payments are made, how long will it take for the amount due to reach \$35,000?
Solution:
(a)
For the interest compounded continuously, you should use the following formula:
$A=P e^{rt}$
$t$ is the number of years, $A$ is the amount after $t$ years, $P$ is the Principal (initial deposit or loan if money is borrowed) and $r$ is the interest rate.
You are given:
$P=4000\:\$$; $r=3.5\%=3.5/100=0.035$; and $t=6$ years. You need to find the amount $A$ after $6$ years. Substituting, $P$,$r$ and $t$ in the equation:
$A=4000 e^{0.035\cdot 6}$
$A=4000 e^{0.035\cdot 6}$
$ =4000 e^{0.21}$
$ =4000 \cdot 1.2337$
$ =4934.71 \:\$$
This is one of the answer.
Next, you need to find how long does it take to double the amount. That is you need to find the time, $t$ to double the amount.
Amount is doubled, so, $A=2P$. Substituting this, $A$ and $r$ in the formula:
$2P=Pe^{0.035t}$
Divide out $P$, and solve for $t$:
$2=e^{0.035t}$
To solve, take $\ln$ on both sides:
$\ln (2)= \ln(e^{0.035t})$
$\ln (2)= 0.035t\,\ln(e)$
Putting, $\ln(e)=1$:
$\ln (2)= 0.035t$
Divide $0.035$ to get $t$:
$t=\ln(2)/0.035=19.8$ years
(b).
The equation for the amount after $t$ years is given
$A(t)=29,000(1.03)^t$.
Initial deposit amount and the interest rate are included in the equation, so don't worry about those numbers.
You need to find the time $t$ to reach the amount, $35,000$.
Substitute, $A=35,000$ and solve for $t$:
$35000=29000(1.03)^t$
Divide $29000$ on both sides to isolate the exponent:
$1.2069=1.03^t$
This is an exponential equation. To solve for $t$, take log on both sides:
$\log(1.2069)=\log(1.03^t)$
$\log(1.2069)=t\,\log(1.03)$
Divide, $\log(1.03)$ on both sides to get $t$:
$\dfrac{\log(1.2069)}{\log(1.03)}=t$
Using the calculator:
$t=6.36$
This is the answer. So, after $6.36$ years, the loan amount will reach \$35,000.
