Practice questions

page1 page2 page3 page4 page5 page6 page7 page8

1. Linear inequalities and absolute value equations

1. Solve the following expressions.

(a) $|y+2|-1=10$

(b) $|2x-1|\ge 7$

(b) $|x+5|-6\le -1$

Solution:

(a).

First isolate the absolute value.

$|y+2|=10\color{blue}+1$

$|y+2|=11$

Solution for the above equation is

$y+2=-11$ or $y+2=11$

Solving for $y$

$y=-11\color{red}-2$ or $y=11\color{red}-2$

$y=-13$ or $y=9$

The solution set is $\{-13, 9\}$

(b).

The absolute value, $|2x-1|$ is greater than or equal to a positive number, $7$.

The solution is

$2x-1\le -7$ or $2x-1\ge 7$

Next, you need to solve for $x$.

Add $1$:

$2x\le -7\color{red}+1$ or $2x\ge 7\color{red}+1$

$2x\le -6$ or $2x\ge 8$

Divide $2$:

$x\le -6/2$ or $x\ge 8/2$

$x\le -3$ or $x\ge 4$

The solution in interval notation:

$(-\infty, -3]\cup [4, \infty)$

(c).

Isolate the absolute value:

$|x+5|\le -1\color{red}+6$

$|x+5|\le 5$

An absolute value is less than or equal to a positive number $5$.

The solution is

$-5\le x+5 \le 5$

Add $-5$

$-5-5 \le x+5-5 \le 5-5$

$-10 \le x \le 0$

In interval notation, the above solution is

$[-10, 0]$

2. Solve and graph the solutions for the following problems. Write the solution in interval notation.

(a) $4-3x\ge 10$ or $5x-2\gt 13$

(b) $7x+4\ge -17$ and $6x+5\ge -7$

Solution:

(a).

Solve for $x$ in each inequality:

$-3x\ge 10\color{red}-4$ or $5x\gt 13\color{red}+2$

$-3x\ge 6$ or $5x\gt 15$

$\dfrac{-3x}{-3}\le \dfrac{6}{-3}$ or $\dfrac{5x}{5}\gt \dfrac{15}{5}$

$x\le -2$ or $x\gt 3$

Graph:

In interval notation:

$[-\infty, -2]\cup(3, \infty)$

(b).

Solve for $x$ in each inequality:

$7x\ge -17\color{red}-4$ and $6x\ge -7 \color{red}-5$

$7x\ge -21$ and $6x\ge -12$

$\dfrac{7x}{7}\ge \dfrac{-21}{7}$ and $\dfrac{6x}{6}\ge \dfrac{-12}{6}$

$x\ge -3$ and $x\ge -2$

Graph:

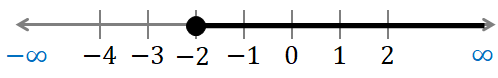
In interval notation:

$[-2, \infty)$