Practice questions

page1 page2 page3 page4 page5 page6 page7 page8

5. Quadratic equations

24. Solve the following equations.

(a) $(t+5)^2=48$

(b) $y^2-14y+49=0$

Solution:

(a).

Use the square root property to solve:

$t+5=\sqrt{48}$ or $t+5=-\sqrt{48}$

Solving for $t$:

$t=-5+\sqrt{48}$ or $t=-5-\sqrt{48}$

Factoring the square root: $\sqrt{48}=\sqrt{16\cdot 3}=4\sqrt{3}$

$t=-5+4\sqrt{3}$ or $t=-5-4\sqrt{3}$

25. Find the value of $c$ such that $9x^2-30x + c = 0$ has exactly one solution.

Solution:

It is given that the quadratic equation has only one solution. So, the discriminant should be zero:

$b^2-4ac=0$

From the given equation, we have $a=9$, $b=-30$ and we need to find $c$. Substitute the values of $a$ and $b$ and solve for $c$:

$(-30)^2-4\cdot 9c=0$

$900-36c=0$

Solving for c:

$c=25$

26. For the quadratic function $f(x)=-2x^2-2x+3$, find the following:

(a) The vertex

(b) The line of symmetry

(d) The x-intercept

(e) The y-intercept

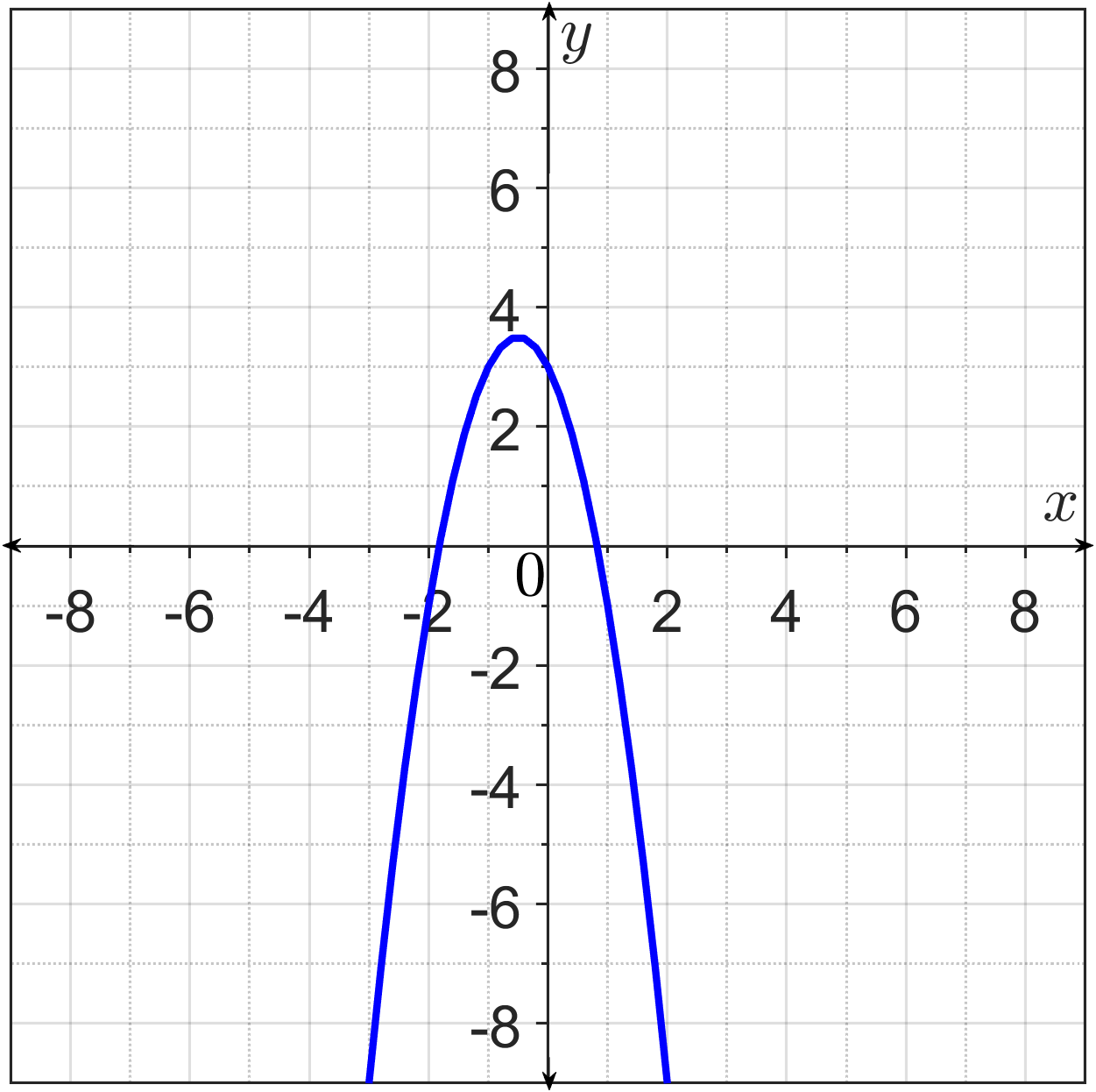
(f) The graph of the function.

Solution:

The quadratic function is

$f(x)=-2x^2-2x+3$

Here, $a=-2$; $b=-2$ and $c=3$

(a).

The vertex is $(h, k)$

We need to find $h$ and $k$:

$h=-\dfrac{b}{2a}=-\dfrac{(-2)}{2(-2)}$

$=-\dfrac{1}{2}$

To find the $k$, substitute $x=-\dfrac{1}{2}$ in the function:

$k=f(-1/2)=-2(-1/2)^2-2\cdot (-1/2)+3$

$=-2\cdot 1/4+1+3$

$=-1/2+4$

$=\dfrac{-1+4\cdot 2}{2}$

$=\dfrac{7}{2}$

So, the vertex is $\left(-\dfrac{1}{2}, \dfrac{7}{2}\right)$

(b).

The equation of the line of symmetry is

$x=h$

Substituting the value of $h$:

$x=-\dfrac{1}{2}$

(c)

$a$ is negative, so the function has a maximum value.

The maximum value of the function is $k$.

Thus the maximum value of the function $=\dfrac{7}{2}$

(d).

To find the $x$ intercept, put $y=0$, $y$ is $f(x)$, so put $f(x)=0$. And solve for $x$:

$-2x^2-2x+3=0$

Change the sign of each term, so that the $x^2$ term is positive:

$2x^2+2x-3=0$

You cannot factor this equation, so, solve the equation by quadratic formula:

$x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$a=2; b=2; c =-3$

$x=\dfrac{-2\pm \sqrt{2^2-4\cdot 2 (-3)}}{2\cdot 2}$

$x=\dfrac{-2\pm \sqrt{4+24}}{4}$

$x=\dfrac{-2\pm \sqrt{28}}{4}$

$x=\dfrac{-2\pm 5.2915}{4}$

$x=\dfrac{-2+ 5.2915}{4}$ or $x=\dfrac{-2- 5.2915}{4}$

$x=0.823$ or $x=-1.823$

These are the $x$-intercepts.

As ordered pairs:

$(0.823,0)$ and $(-1.823, 0)$

(e).

To find the $y$-intercept, put $x=0$, and find y:

$y=f(0)=-2\cdot 0^2-2\cdot 0+3=3$

As ordered pair, the y-intercept is $(0, 3)$.

(f).

Graph:

27. A club swimming pool is 30 feet long. The area of the pool is 1200 ft². The club members want a paved walkway with uniform width around the pool. They have enough material to cover 296 ft². How wide can the strip be?

Solution:

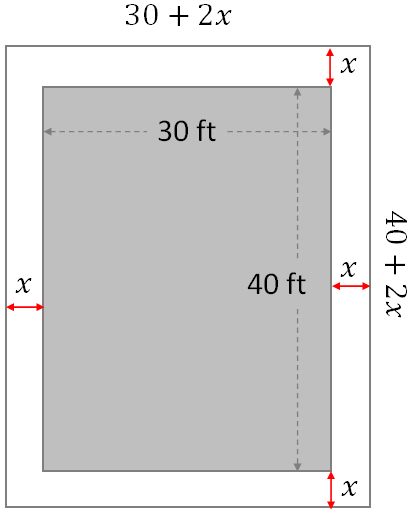
Given, the area of the pool is 1200 ft²; and the length of the pool is 300 ft. From these we can find the breadth of of the pool:

$\textup{breadth}=\dfrac{\textup{Area}}{\textup{length}}=\dfrac{1200}{30}=40$ ft.

Let $x$ is the width of the walkway that we need to find.

From the figure, the area of the walkway

$=$Total area of the pool and the walkway $-$Area of the pool

$=(40+2x)(30+2x)-1200$

$=1200+80x+60x+4x^2-1200$

$=140x+4x^2$

This area can be equal to or less than the available material of area 296 ft². So, for the maximum area,

$140x+4x^2=296$

This is a quadratic equation, move everything to one side and solve for $x$:

$4x^2+140x-296=0$

$4$ is the common factor, you can divide that out:

$x^2+35x-74=0$

Factor and solve this:

$(x+37)(x-2)=0$

$x=-37$ or $ x= 2$

$x$ is the width of the walkway that cannot be negative. So, the only solution is $x=2$.

So, the maximum width of the pathway is $2$ ft. Thus, width can be 2ft or smaller.