Linear inequalities in one variable
An inequality is a sentence that contains <, ≤, > or ≥.Examples:
$x\lt 5$
$2x-3\le 4$
$7y-1\gt 4(3y-1)$
$-9y+1\ge 2-4y$
The above inequalities have only one variable $x$ or $y$, so they are inequalities in one variable.
Like an equation, an inequality has solution.
For the inequality, $x\lt 2$, the solution is all real numbers less than $2$.
You can graph the solution on a number line, or write it in the interval notation or in the set-builder notation.
Graph of $x<2$:
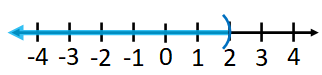
Instead of parenthesis, you can also use open circle as below.
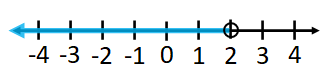
In the interval notation, $x\lt 2$ is $(-\infty, 2)$.
In the set-builder notation, $x\lt 2$ is $\{x|x\lt 2\}$.
Graph of $x\le 2$:
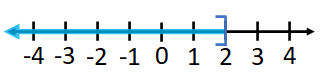
Instead of the bracket, you can also use a filled circle as in the figure below,
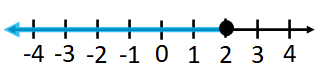
Here also, instead of the
For the $x\le 2$, the interval notation is $(-\infty, 2]$.
And the set-builder notation is $\{x|x\le 2\}$.
Graph of $x\gt 2$,
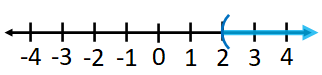
For the $x\gt 2$, the interval notation is $(2, \infty)$.
And the set-builder notation is $\{x|x\gt 2\}$.
Graph of $x\ge 2$,
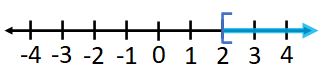
For the $x\ge 2$, the interval notation is $[2, \infty)$.
And the set-builder notation is $\{x|x\ge 2\}$.
Note that if there is an equal sign with the inequality, then use the bracket (or a filled circle), if no equal sign, then use the parenthesis (or a open circle). For infinity ($\infty$ or $-\infty$), always use parenthesis.
Solving linear inequality
Solving an inequality means, isolating the variable, and then graphing the solution on a number line, or writing the solution in the interval or set-builder notation. To solve an inequality, you will use the following properties of inequality.Addition and subtraction properties of inequality
For any real numbers, $a$, $b$ and $c$,If $a\lt b$ then
$a+c\lt b+c$
and$a-c\lt b-c$
Multiplication and division properties of inequality
For any real numbers $a, b$ and $c$,if $a\lt b$ then
$ac\lt bc$ if $c$ is positive.
$ac\gt bc$ if $c$ is negative.
and$\dfrac{a}{c}\lt \dfrac{b}{c}$ if $c$ is positive.
$\dfrac{a}{c}\gt \dfrac{b}{c}$ if $c$ is negative.
Note that if you multiply/divide a negative number, the sign of the inequality changes. i.e., $\lt$, becomes, $\gt$ and vice versa.
If you switch the sides, i.e., move everything on the right side to the left side and everything on the left to the right side, then you need to switch the inequality sign. i.e.,
$4\lt x \:$ is same as $\: x \gt 4$
$y\ge -4 \:$ is same as $\: -4 \le y$
Example 1: Solve, $3x+6\ge 9$
Solution:
$\begin{align*} 3x+6\quad &\ge 9\\ -6:\quad 3x\quad &\ge 9-6\\ \qquad 3x\quad &\ge 3\\ \div 3:\quad x\quad &\ge 1 \end{align*}$Solution in interval notation is
$[1,\infty)$Example 2: Solve, $14+6y\gt 2+9y$
Solution:
$\begin{align*} 14+6y\quad &\gt \quad 2+9y\\ -9y:\quad 14-3y\quad &\gt \quad 2\\ -14:\qquad -3y\quad &\gt \quad -12\\ \div -3:\qquad y\quad &\lt \quad 4\\ \end{align*}$Solution in interval notation is
$(-\infty, 4)$Compound inequalities
Two inequalities, which are joined with the word 'or' or the word 'and' is called compound inequality.Examples of compound inequalities:
$x\le 5 \quad or \quad 5\gt 2x +1$
$8\gt x-2 \quad and \quad x\le 7$
A compound inequality of the form:$a\lt x\lt b$ is same as $a\lt x$ and $x\lt b$. This means $x$ is between $a$ and $b$.
In interval notation, $a\lt x\lt b$ is $(a,b)$ and
$a\le x\le b$ is $[a,b]$.
The word 'or' corresponds to the union operation and the word 'and' corresponds to the intersection operation.
Union
If $A$ and $B$ are two sets, then the union of $A$ and $B$ is the set of elements which are in $A$ or in $B$ or in both $A$ and $B$.
Union of $A$ and $B$ or $A$ union $B$ is denoted as $A\cup B$.
Union operation combines the two sets.
Example:If $A=\{1,2,3,4,5\}$, and $B=\{3,4,7,8\}$, then
$A\cup B=\{1,2,3,4,5,7,8\}\:$ ---combine A and B.
Example:Find the union of the sets A and B, where $A=\{x|x\lt -2\}$ and $B=\{x|x\ge 3\}$.
Solution: Draw the graph of $A$ and $B$ and combine them:
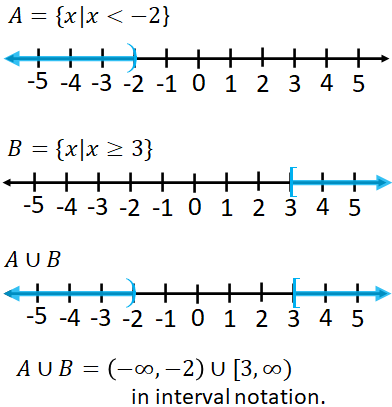
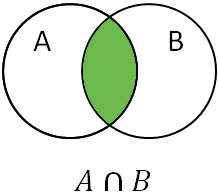
Intersection
If $A$ and $B$ are two sets, then the intersection of $A$ and $B$ is the set of elements which are common to both $A$ and $B$.
Intersection of $A$ and $B$ or $A$ intersection $B$ is denoted as $A\cap B$.
Intersection operation extracts the elements common to both the sets.
Example 1:If $A=\{1,2,3,4,5\}$, and $B=\{3,4,7,8\}$, then
$A\cap B=\{3,4\}\:$ only 3 & 4 are in both $A$ and $B$.
Example 2: If $P=\{a, b, c\}$ and $Q=\{e, f, g\}$, then
$P\cap Q=\{\quad \}$, the empty set. The symbol for the empty set is $\emptyset$.
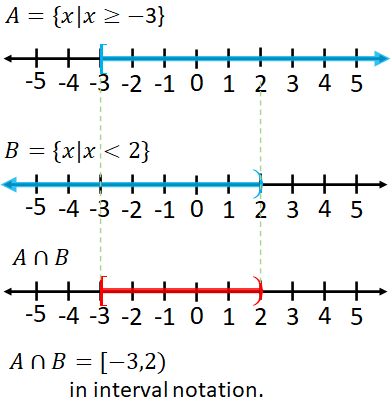
Example:Find the intersection of the sets A and B, where $A=\{x|x\ge -3\}$ and $B=\{x|x\lt 2\}$.
Solution: Draw the graph of $A$ and $B$ and take the part of the solution common to both:
Solving compound inequalities
To solve a compound inequality, solve the individual inequalities separately and take the union of the solutions if the inequalities are joined by the word or; or take the intersection of the solutions, if the inequalities are joined by the word and.Example:1 Solve, $4x\lt x-6$ or $x\ge 3$
Solution:$\begin{align*} 4x\lt x-6 \, &or\ x\ge 3\\ -x:\quad 4x-x\lt -6 \, &or \, x\ge 3\\ \div 3: \qquad x\lt -2 \, &or\, x\ge 3 \end{align*}$
Solution in graphical form:
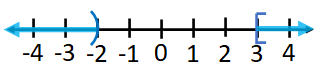
Solution in interval notation:
$(-\infty,-2)\cup[3,\infty)$
Example 2: Solve $4x-2\lt 14$ and $2x\ge 2$
solution:$\begin{align*} 4x-2\lt 14\quad &and \quad2x\ge 2\\ 4x\lt 16\quad &and \quad x\ge 1\\ x\lt 4\quad &and \quad x\ge 1 \end{align*}$
The solution in the graphical form:
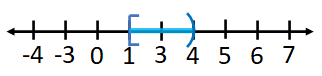
The solution in interval notation:
$[1,4)$
Absolute value equations and inequalities
Absolute value of a number is the distance of the number from zero on the number line. Since distance is always positive, absolute value is always positive. Absolute value of a number, $A$ is written as $|A|$.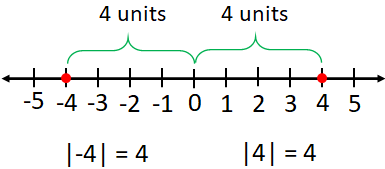
Solving absolute value equation
If $|X|=a$ then $X=a$ or $X=-a$ if $a$ is positive or zero.Example 1: Solve for $x$, $|x|=3$.
Solution:$x=3$ or $x=-3$
Solution is $\{3,-3\}$.Example 2: Solve for $u$, $|u-2|=3$.
Solution:$u-2=3$ or $u-2=-3$
Simplifying,$u=5$ or $u=-1$
Solution is $\{5,-1\}$.If $|x|=a$ then there is no solution if $a$ is negative.
Example 1: Solve for $y$, $|y|=-7$
Solution:There is no solution.
i.e., the solution is empty set, the symbol for the empty set is $\emptyset$.Example 2: Solve for $x$, $|2x-1|=-6$
Solution:There is no solution.
i.e., the solution is $\emptyset$.Equality of absolute values
If $|X|=|Y|$, then $X=Y$ or $X=-Y$.Solving absolute value inequalities
For any positive real number, $a$,if $|X|\lt a$, then $-a\lt X\lt a$
if $|X|\le a$, then $-a\le X\le a$
if $|X|\gt a$, then $X\lt -a\:$ or $\:X\gt a$
if $|X|\ge a$, then $X\le -a\:$ or $\:X\ge a$
For any negative number $a$,
$|X|\lt a$, has no solution.
$|X|\le a$, has no solution.
and
$|X|\gt a$, is true for all values of $X$.
$|X|\ge a$, is true for all values of $X$.
